Using Bayesian Networks to forecast ancillary service volume in hospitals

A Python example using diagnostic input variables

Since I’ve been working with healthcare data (almost 10 years now), forecasting future patient volume has been a tough nut to crack. There are so many dependencies to consider — patient requests and severity, administrative needs, exam room constraints, a provider just called out sick, a bad snow storm. Plus, unanticipated scenarios can have cascading impacts on scheduling and resource allocation that contradict even the best Excel projections.

These kinds of problems are really interesting to try and solve from a data perspective, one because they’re tough and you can chew on it for awhile, but also because even slight improvements can lead to major wins (e.g., improve patient throughput, lower wait times, happier providers, lower costs).

How to solve it then? Well, Epic provides us with lots of data, including actual records of when patients arrived for their appointments. With historical outputs known, we’re mainly in the space of supervised learning, and Bayesian Networks (BNs) are good probabilistic graphical models.

While most decisions can be made on a single input (e.g., “should I bring a raincoat?”, if the input is “it’s raining”, then the decision is “yes”), BNs can easily handle more complex decision-making — ones involving multiple inputs, of varying probability and dependencies. In this article, I’m going to “scratch pad” in python a super simple BN that can output a probability score for a patient arriving in 2 months based on known probabilities for three factors: symptoms, cancer stage, and treatment goal.

Understanding Bayesian Networks:

At its core, a Bayesian Network is a graphical representation of a joint probability distribution using a directed acyclic graph (DAG). Nodes in the DAG represent random variables, and directed edges denote causal relationships or conditional dependencies between these variables. As is true for all data science projects, spending lots of time with the stakeholder in the beginning to properly map the workflows (e.g., variables) involved in decision-making is critical for high-quality predictions.

So, I’ll invent a scenario that we meet our Breast oncology partners and they explain that three variables are critical for determining whether a patient will need an appointment in 2 months: their symptoms, cancer stage, and treatment goal. I’m making this up as I type, but let’s go with it.

(In reality there will be dozens of factors that influence future patient volumes, some of singular or multiple dependencies, others completely independent but still influencing).

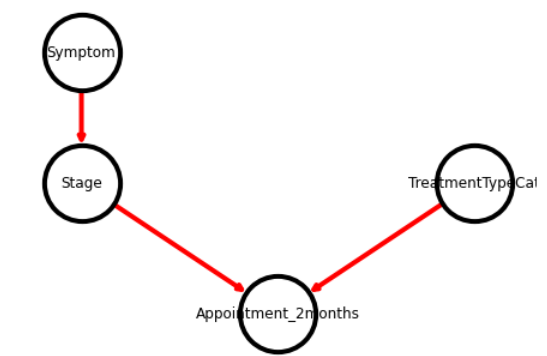
I’ll say the workflow looks like the above: Stage depends on their symptom, but treatment type is independent of those and also influences the appointment occurring in 2 months.

Based on this, we would the fetch data for these variables from our data source (for us, Epic), which again, would contain known values for our score node (Appointment_2months), labeled “yes” or “no”.

# install the packages
import pandas as pd # for data manipulation 
import networkx as nx # for drawing graphs
import matplotlib.pyplot as plt # for drawing graphs

!pip install pybbn
# for creating Bayesian Belief Networks (BBN)
from pybbn.graph.dag import Bbn
from pybbn.graph.edge import Edge, EdgeType
from pybbn.graph.jointree import EvidenceBuilder
from pybbn.graph.node import BbnNode
from pybbn.graph.variable import Variable
from pybbn.pptc.inferencecontroller import InferenceController

# Create nodes by manually typing in probabilities
Symptom = BbnNode(Variable(0, 'Symptom', ['Non-Malignant', 'Malignant']), [0.30658, 0.69342])
Stage = BbnNode(Variable(1, 'Stage', ['Stage_III_IV', 'Stage_I_II']), [0.92827, 0.07173, 
                                                      0.55760, 0.44240])
TreatmentTypeCat = BbnNode(Variable(2, 'TreatmentTypeCat', ['Adjuvant/Neoadjuvant', 'Treatment', 'Therapy']), [0.58660, 0.24040, 0.17300])
Appointment_2weeks = BbnNode(Variable(3, 'Appointment_2weeks', ['No', 'Yes']), [0.92314, 0.07686, 
                                                0.89072, 0.10928, 
                                                0.76008, 0.23992, 
                                                0.64250, 0.35750, 
                                                0.49168, 0.50832, 
                                                0.32182, 0.67818])

Above, let’s manually input some probability scores for levels in each variable (node). In practice, you’d use a crosstab to achieve this.

For example, for the symptom variable, I’ll get frequencies of their 2-levels, about 31% are non-malignant and 69% are malignant.

Then, we consider the next variable, Stage, and crosstab that with Symptom to get these freqeuncies.

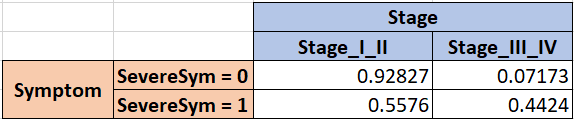
And, so on and so forth, until all crosstabs between parent-child pairs are defined.

Now, most BNs include many parent-child relationships, so calculating probabilities can get tedious (and majorly error prone), so the function below can calculate the probability matrix for any child node corresponding with 0, 1 or 2 parents.

# This function helps to calculate probability distribution, which goes into BBN (note, can handle up to 2 parents)
def probs(data, child, parent1=None, parent2=None):
    if parent1==None:
        # Calculate probabilities
        prob=pd.crosstab(data[child], 'Empty', margins=False, normalize='columns').sort_index().to_numpy().reshape(-1).tolist()
    elif parent1!=None:
            # Check if child node has 1 parent or 2 parents
            if parent2==None:
                # Caclucate probabilities
                prob=pd.crosstab(data[parent1],data[child], margins=False, normalize='index').sort_index().to_numpy().reshape(-1).tolist()
            else:    
                # Caclucate probabilities
                prob=pd.crosstab([data[parent1],data[parent2]],data[child], margins=False, normalize='index').sort_index().to_numpy().reshape(-1).tolist()
    else: print("Error in Probability Frequency Calculations")
    return prob  

Then we create the actual BN nodes and the network itself:

# Create nodes by using our earlier function to automatically calculate probabilities
Symptom = BbnNode(Variable(0, 'Symptom', ['Non-Malignant', 'Malignant']), probs(df, child='SymptomCat'))
Stage = BbnNode(Variable(1, 'Stage', ['Stage_I_II', 'Stage_III_IV']), probs(df, child='StagingCat', parent1='SymptomCat'))
TreatmentTypeCat = BbnNode(Variable(2, 'TreatmentTypeCat', ['Adjuvant/Neoadjuvant', 'Treatment', 'Therapy']), probs(df, child='TreatmentTypeCat'))
Appointment_2months = BbnNode(Variable(3, 'Appointment_2months', ['No', 'Yes']), probs(df, child='Appointment_2months', parent1='StagingCat', parent2='TreatmentTypeCat'))

# Create Network
bbn = Bbn() 
    .add_node(Symptom) 
    .add_node(Stage) 
    .add_node(TreatmentTypeCat) 
    .add_node(Appointment_2months) 
    .add_edge(Edge(Symptom, Stage, EdgeType.DIRECTED)) 
    .add_edge(Edge(Stage, Appointment_2months, EdgeType.DIRECTED)) 
    .add_edge(Edge(TreatmentTypeCat, Appointment_2months, EdgeType.DIRECTED))

# Convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)

And we’re all set. Now let’s run some hypotheticals through our BN and evaluate the outputs.

Evaluating the BN outputs

First, let’s take a look at the probability of each node as it stands, without specifically declaring any conditions.

# Define a function for printing marginal probabilities
# Probabilities for each node
def print_probs():
    for node in join_tree.get_bbn_nodes():
        potential = join_tree.get_bbn_potential(node)
        print("Node:", node)
        print("Values:")
        print(potential)
        print('----------------')
        
# Use the above function to print marginal probabilities
print_probs()

Node: 1|Stage|Stage_I_II,Stage_III_IV
Values:
1=Stage_I_II|0.67124
1=Stage_III_IV|0.32876
----------------
Node: 0|Symptom|Non-Malignant,Malignant
Values:
0=Non-Malignant|0.69342
0=Malignant|0.30658
----------------
Node: 2|TreatmentTypeCat|Adjuvant/Neoadjuvant,Treatment,Therapy
Values:
2=Adjuvant/Neoadjuvant|0.58660
2=Treatment|0.17300
2=Therapy|0.24040
----------------
Node: 3|Appointment_2weeks|No,Yes
Values:
3=No|0.77655
3=Yes|0.22345
----------------

Meaning, all the patients in this dataset have a 67% probability of being Stage_I_II, a 69% probability of being Non-Malignant, a 58% probability of requiring Adjuvant/Neoadjuvant treatment, and only 22% of them required an appointment 2 months from now.

We could easily get that from simple frequency tables without a BN.

But now, let’s ask a more conditional question: What’s the probability a patient will require care in 2 months given that they have Stage = Stage_I_II and have a TreatmentTypeCat = Therapy. Also, consider the fact that the provider knows nothing about their symptoms yet (maybe they haven’t seen the patient yet).

We’ll run what we know to be true in the nodes:

# To add evidence of events that happened so probability distribution can be recalculated
def evidence(ev, nod, cat, val):
    ev = EvidenceBuilder() 
    .with_node(join_tree.get_bbn_node_by_name(nod)) 
    .with_evidence(cat, val) 
    .build()
    join_tree.set_observation(ev)

# Add more evidence
evidence('ev1', 'Stage', 'Stage_I_II', 1.0)
evidence('ev2', 'TreatmentTypeCat', 'Therapy', 1.0)
# Print marginal probabilities
print_probs()

Which returns:

Node: 1|Stage|Stage_I_II,Stage_III_IV
Values:
1=Stage_I_II|1.00000
1=Stage_III_IV|0.00000
----------------
Node: 0|Symptom|Non-Malignant,Malignant
Values:
0=Non-Malignant|0.57602
0=Malignant|0.42398
----------------
Node: 2|TreatmentTypeCat|Adjuvant/Neoadjuvant,Treatment,Therapy
Values:
2=Adjuvant/Neoadjuvant|0.00000
2=Treatment|0.00000
2=Therapy|1.00000
----------------
Node: 3|Appointment_2months|No,Yes
Values:
3=No|0.89072
3=Yes|0.10928
----------------

That patient only has an 11% chance of arriving in 2 months.

A note about the importance of quality input variables:

The success of a BN in providing a reliable future visit estimate depends heavily on an accurate mapping of workflows for patient care. Patients presenting similarly, in similar conditions, will typically require similar services. The permutation of those inputs, whose characteristics can span from the clinical to administrative, ultimately correspond to a somewhat deterministic path for service needs. But the more complicated or farther out the time projection, the higher the need for more specific, intricate BNs with high-quality inputs.

Here’s why:

1. Accurate Representation: The structure of the Bayesian Network must reflect the actual relationships between variables. Poorly chosen variables or misunderstood dependencies can lead to inaccurate predictions and insights.
2. Effective Inference: Quality input variables enhance the model’s ability to perform probabilistic inference. When variables are accurately connected based on their conditional dependence, the network can provide more reliable insights.
3. Reduced Complexity: Including irrelevant or redundant variables can unnecessarily complicate the model and increase computational requirements. Quality inputs streamline the network, making it more efficient.

Thanks for reading. Happy to connect with anyone on LinkedIn! If you are interested in the intersection of data science and healthcare or if you have interesting challenges to share, please leave a comment or DM.

Check out some of my other articles:

Why Balancing Classes is Over-Hyped

Feature Engineering CPT Codes

7 Steps to Design a Basic Neural Network

Using Bayesian Networks to forecast ancillary service volume in hospitals was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.